Predicción múltiple de token: razonamiento algorítmico de maestría con uso mejorado de recursos

Tabla de enlaces

Resumen y 1. Introducción

2. Método

3. Experimentos sobre datos reales

4. Ablaciones en datos sintéticos

5. ¿Por qué funciona? Algunas especulaciones

6. Trabajo relacionado

7. Conclusión, declaración de impacto, impacto ambiental, reconocimientos y referencias

A. Resultados adicionales sobre la decodificación autoespeculativa

B. Arquitecturas alternativas

C. velocidades de entrenamiento

D. Finetuning

E. Resultados adicionales en el comportamiento de escala del modelo

F. Detalles sobre CodeContests Finetuning

G. Resultados adicionales en puntos de referencia del lenguaje pure

H. Resultados adicionales sobre resumen de texto abstractivo

I. Resultados adicionales sobre razonamiento matemático en lenguaje pure

J. Resultados adicionales sobre el aprendizaje de inducción

Okay. Resultados adicionales sobre razonamiento algorítmico

L. Intuiciones adicionales sobre la predicción múltiple

M. Entrenamiento de hiperparámetros

Okay. Resultados adicionales sobre razonamiento algorítmico

Investigamos lo siguiente Hipótesis de compartir el cálculo para explicar la eficacia de la predicción múltiple como pérdida de entrenamiento.

La dificultad de predicción de diferentes tokens en el texto pure varía mucho. Algunos tokens pueden ser las continuaciones de palabras parciales que se determinan de manera única a partir de su contexto anterior sin ningún esfuerzo, mientras que otros pueden requerir los nombres de los teoremas en pruebas matemáticas difíciles o la respuesta correcta a una pregunta del examen. Se ha demostrado que los modelos de lenguaje con conexiones residuales refinan su distribución de tokens de salida con cada capa sucesiva, y pueden ser entrenados con estrategias de salida temprana que gastan cantidades variables de recursos computacionales por posición de token. Las pérdidas de predicción de múltiples token fomentan explícitamente el intercambio de información entre las posiciones de token adyacentes y, por lo tanto, pueden verse como un método para aprender la asignación de recursos computacionales en los modelos de lenguaje de manera más eficiente a los tokens que benefician a la mayor parte.

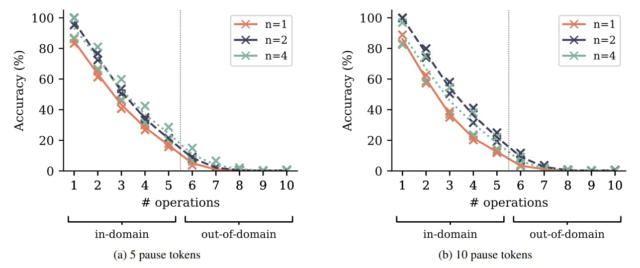
Para verificar la verdad de esta hipótesis, aumentamos la tarea aritmética polinomial de la Sección 4.2 con un número variable de tokens de pausa (Goyal et al., 2023) Insertado entre la pregunta y un token que denota el comienzo de la respuesta. Los tokens de pausa introducen recursos computacionales adicionales que se pueden gastar para los cálculos que se espera que sean útiles más adelante en la secuencia, en otras palabras: para comenzar a pensar en la respuesta. Según el Hipótesis de compartir el cálculolos modelos de predicción de múltiples token aprenden a compartir información y, por lo tanto, el intercambio de cálculos entre las posiciones de token más fácilmente, y puede ser mejor para utilizar estos recursos computacionales adicionales que los modelos de predicción de los próximos token. En la Figura S15, mostramos los resultados de la evaluación en la tarea aritmética polinomial con un número fijo de tokens de pausa insertados tanto en el tiempo de entrenamiento como de evaluación. Los modelos de predicción de múltiples token también superan a los modelos de predicción de la siguiente token en estas variantes de tareas a través de dificultades de tareas y tamaños de modelos. Sin embargo, no vemos una fuerte evidencia de una ampliación o reducción de esta brecha, es decir, no podemos concluir de estos experimentos sobre la veracidad de la hipótesis de compartir el cálculo.

En la Tabla S11, informamos los resultados de otro experimento con el mismo espíritu: al agregar espacios y nuevas líneas a las indicaciones humaneval y MBPP, agregamos “tokens de pausa” de una manera algo pure. Según estos resultados, los modelos de predicción de múltiples token tienen una ligera ventaja en el uso de este cómputo provisto adicionalmente, pero el efecto es marginal.