Tabla de enlaces
-
Introducción
-
Prueba de hipótesis
2.1 Introducción
2.2 Estadísticas bayesianas
2.3 Check Martingales
2.4 Valores P
2.5 paradas y miradas opcionales
2.6 Combinación de valores P y continuación opcional
2.7 pruebas A/B
-
Pruebas seguras
3.1 Introducción
3.2 Check Classical T
3.3 Testia t segura
3.4 χ2 -test
3.5 Prueba de proporción segura
-
Simulaciones de pruebas seguras
4.1 Introducción e implementación de 4.2 Python
4.3 Comparación de la prueba t con la prueba t segura
4.4 Comparación de la prueba χ2 con la prueba de proporción segura
-
Prueba de relación de probabilidad secuencial de mezcla
5.1 Pruebas secuenciales
5.2 Mezcla SPRT
5.3 MSPRT y la prueba t segura
-
Experimentos controlados en línea
6.1 Check T Secure en OCE DataSets
-
Pruebas A/B vinculadas y 7,1 prueba t segura para pruebas A/B vintadas
7.2 Prueba de proporción segura para la relación de la relación de muestra.
-
Conclusión y referencias
4 simulaciones de pruebas seguras
4.1 Introducción
En esta sección, comparamos la prueba t clásica con la prueba t segura y la prueba χ2 con la prueba de proporción segura. Se ha desarrollado una biblioteca exhaustiva para pruebas seguras en R [LTT20]. Con el objetivo de aumentar la adopción en el campo de la ciencia de datos, portamos el código para la prueba t segura y la prueba de proporción segura en Python.
4.2 Implementación de Python
Si bien la lógica de la prueba t segura sigue siendo la misma, hubo una serie de ineficiencias en el código unique que debía abordarse para trabajar con tamaños de muestra grandes. Las mejoras se detallan aquí.
La primera mejora se produce para determinar el tamaño de la muestra requerido para un proceso por lotes de los datos. La función unique realiza una búsqueda lineal de 1 a un número alto arbitrario. Para cada posible tamaño de muestra en el rango, la función calcula el valor E en función de los tamaños de muestra, los grados de libertad y el tamaño del efecto. El bucle se rompe cuando el valor E es mayor que 1/α. Dado que esta es una función monotónicamente que aumenta, una búsqueda binaria acelera considerablemente el cálculo, reduciendo la complejidad computacional de O (N) a O (log N). Esta optimización demostró ser necesaria cuando se trabajaba con millones de muestras.
La siguiente mejora de la velocidad necesaria es calcular el tiempo de detención para una potencia de 1 – β. Esto se determina mediante la simulación de datos que difieren por el tamaño del efecto mínimo. En el transcurso de N simulaciones, los datos de la longitud M se transmiten individualmente para determinar el punto en el que el valor E cruza 1/α. Una vez más, este proceso se realiza a través de una búsqueda lineal. Para optimizar esta función, el cálculo del martingale está paralelo a todo el vector de longitud m. La complejidad computacional sigue siendo O (NM), pero el cálculo vectorial tiene lugar en el código Numpy, a diferencia de un bucle de pitón. El código Numpy está escrito en C, por lo tanto, el cálculo es mucho más rápido.
La modificación last no es reducir la complejidad computacional, sino en mejorar las capacidades de la prueba de proporción segura. Esta prueba se escribió en R como una prueba de dos muestras con tamaños de lotes fijos. Para nuestro caso de uso, se requirió una prueba de una muestra con tamaños de lotes variables para detectar la relación de desajuste de muestra y, por lo tanto, se desarrolló para el paquete Python.
4.3 Comparación de la prueba t con la prueba t segura
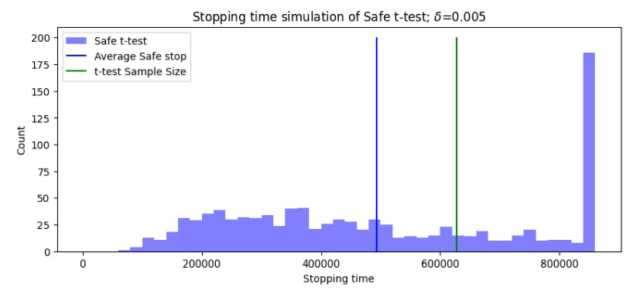
La forma más directa de comprender la prueba t segura es compararla con su alternativa clásica. Realizamos simulaciones de un tamaño de efecto δ y una hipótesis nula H0: δ = 0. Estableciendo el nivel de significancia α = 0.05 podemos simular un tamaño de efecto δ entre dos grupos para determinar cuándo se detiene la prueba. Si el valor E simulado cruza 1/α = 20, la prueba se detiene con H0 rechazada. Si no se detecta ningún efecto, la prueba se detiene a una potencia de 1 – β = 0.8, ya que este poder es común dentro de la industria. La Figura 3 muestra simulaciones de tiempos de detención y decisiones de la prueba segura en comparación con la prueba t.
Como podemos ver en los tiempos de detención promedio en la Figura 3, la prueba t segura usa menos de 500,000 muestras para entregar resultados estadísticamente válidos, mientras que la prueba t clásica requiere más de 600,000. Sin embargo, el tamaño de la muestra requerido para alcanzar la potencia de 1-β para la prueba t segura es de aproximadamente 850,000, mucho mayor que el de la prueba t clásica. Uno puede preguntarse si es aceptable simplemente realizar la prueba t segura hasta el tamaño clásico de la muestra t de la prueba. La Figura 4 (izquierda) muestra el impacto de esta acción en los errores estadísticos. Al finalizar la prueba, tanto la prueba t clásica como la prueba t segura cumplen con el requisito de que los errores de tipo I estén por debajo de α = 0.05 y los errores de tipo II están por debajo de β = 0.2. Sin embargo, la combinación de las dos pruebas da como resultado una tasa de error inflada tipo I y, por lo tanto, no cumplirá con el nivel esperado de significación estadística del experimentador. Dados los ahorros en la duración de la prueba, puede haber una motivación para desarrollar métodos combinar estas pruebas en el futuro de modo que la tasa de falsos positivos permanezca por debajo de α, por ejemplo, utilizando la corrección de Bonferroni.
Además de las conclusiones generales de las dos pruebas, es interesante considerar los experimentos para los cuales la prueba t clásica y la prueba t segura no están de acuerdo. Como se ve en la Figura 4 (derecha), mientras que ambas pruebas alcanzan el 80% de potencia, lo hacen de maneras muy diferentes. Muchas simulaciones para las cuales la prueba t clásica acepta H0 son rechazadas por la prueba t segura, y viceversa. Esta diferencia en los resultados probablemente será difícil de internalizar para los profesionales que consideran
La prueba t para ser la fuente de la verdad para su plataforma.
Si bien la Figura 3 evalúa los tiempos de parada seguros para un tamaño de efecto fijo, es importante considerar los resultados para una amplia gama de tamaños de efecto. Para agregar los resultados de los tamaños del efecto de 0.01 a 0.3, normalizamos los tiempos de detención por el tiempo de detención de la prueba T. Los resultados de este análisis se pueden ver en la Figura 5.
La gráfica de la Figura 5 muestra la parada promedio de la prueba t segura y el tamaño de la muestra requerido para el 80% de potencia. En promedio, la prueba segura utiliza un 18% menos de datos que la prueba t. Sin embargo, para lograr la misma potencia del 80%, la prueba segura utiliza un 36% más de datos. Dado que la mayoría de las pruebas A/B no dan como resultado el rechazo de H0 [Aze+20]esto podría dar lugar a experimentos más largos en normal para los profesionales.
4.4 Comparación de la prueba χ2 con la prueba de proporción segura
Los resultados de la Figura 6 son notablemente similares a los vistos que comparan la prueba t y la prueba t segura en la Figura 3. La prueba segura nuevamente usa menos muestras, en promedio, que su alternativa clásica, mientras que el tiempo de detención máximo para lograr la potencia requerida es mayor. A continuación, consideramos los tamaños de muestra de las pruebas en función de la diferencia ϵ. La Figura 7 muestra los tiempos de parada promedio y máximo para ϵ ∈ [0001, 0.1].
Como se ve en la Figura 7, el tamaño de muestra promedio requerido para la prueba de proporción segura es menor que el de la prueba χ2 para todos los valores de ϵ. Esto sugiere que la prueba de proporción segura será competitiva con la prueba χ2, incluso para detectar pequeños efectos. Al observar estos resultados, uno puede cuestionar si es apropiado establecer un anterior basado en un tamaño de efecto desconocido. Sin embargo, el Prior puede basar el tamaño del efecto calculado a partir de los datos después de cada muestra. Por lo tanto, establecer los antecedentes en función del tamaño del efecto precise no tiene impacto en la validez de la prueba.
En esta sección, hemos comparado la prueba t segura y la prueba de proporción segura con sus alternativas clásicas. Se encontró que los tamaños de muestra promedio para la prueba t segura son más pequeños que los de la prueba t clásica para un amplio rango de tamaños de efecto. Sin embargo, el tamaño máximo de la muestra puede ser mucho mayor para lograr el mismo poder estadístico. Además, los tamaños de muestra promedio de la prueba de proporción segura son más pequeños que los de la prueba χ2. Estos hallazgos motivan una mayor adopción de pruebas seguras en esfuerzos científicos. En la siguiente sección, comparamos la prueba t segura con otra prueba de cualquier tiempo válido utilizada en la industria, la prueba de relación de probabilidad secuencial de la mezcla.
Autor:
(1) Daniel Beasley
Este documento es