Descripción normal del contenido
- Configuración
- Management de grabación de gradiente
- Dejar de grabar
- Restablecer/comenzar a grabar desde cero
- Detener el flujo de gradiente con precisión
- Gradientes personalizados
- Gradientes personalizados en SavedModel
- Múltiples cintas
- Gradientes de orden superior
- Jacobianos
- Fuente escalar
- Fuente del tensor
- Lote jacobiano
La introducción a los gradientes y la guía de diferenciación automática incluye todo lo requerido para calcular los gradientes en TensorFlow. Esta guía se centra en características más profundas y menos comunes del tf.GradientTape API.
Configuración
import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['figure.figsize'] = (8, 6)
2024-08-15 02:32:10.761137: E exterior/local_xla/xla/stream_executor/cuda/cuda_fft.cc:485] Unable to register cuFFT manufacturing facility: Trying to register manufacturing facility for plugin cuFFT when one has already been registered
2024-08-15 02:32:10.782161: E exterior/local_xla/xla/stream_executor/cuda/cuda_dnn.cc:8454] Unable to register cuDNN manufacturing facility: Trying to register manufacturing facility for plugin cuDNN when one has already been registered
2024-08-15 02:32:10.788607: E exterior/local_xla/xla/stream_executor/cuda/cuda_blas.cc:1452] Unable to register cuBLAS manufacturing facility: Trying to register manufacturing facility for plugin cuBLAS when one has already been registered
Management de grabación de gradiente
En la Guía de diferenciación automática, vio cómo controlar qué variables y tensores son observados por la cinta mientras construye el cálculo del gradiente.
La cinta también tiene métodos para manipular la grabación.
Dejar de grabar
Si desea dejar de grabar gradientes, puede usar tf.GradientTape.stop_recording para suspender temporalmente la grabación.
Esto puede ser útil para reducir la sobrecarga si no desea diferenciar una operación complicada en el medio de su modelo. Esto podría incluir calcular una métrica o un resultado intermedio:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
x_sq = x * x
with t.stop_recording():
y_sq = y * y
z = x_sq + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, form=(), dtype=float32)
dz/dy: None
WARNING: All log messages earlier than absl::InitializeLog() is named are written to STDERR
I0000 00:00:1723689133.642575 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689133.646496 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689133.650243 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689133.653354 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689133.664545 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689133.668230 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689133.671627 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689133.674592 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689133.677498 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689133.680982 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689133.684370 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689133.687370 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.924735 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.926905 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.928886 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.930883 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.932919 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.934914 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.936798 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.938737 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.940666 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.942634 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.944517 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.946466 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.984712 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.986787 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.988685 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.990637 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.993156 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.995163 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.997026 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689134.998929 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689135.000885 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689135.003378 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689135.005704 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
I0000 00:00:1723689135.008045 116670 cuda_executor.cc:1015] profitable NUMA node learn from SysFS had adverse worth (-1), however there have to be at the very least one NUMA node, so returning NUMA node zero. See extra at
Restablecer/comenzar a grabar desde cero
Si desea comenzar por completo, use tf.GradientTape.reset. Simplemente salir del bloque de cintas de gradiente y reiniciar generalmente es más fácil de leer, pero puede usar el reset El método al salir del bloque de cintas es difícil o imposible.
x = tf.Variable(2.0)
y = tf.Variable(3.0)
reset = True
with tf.GradientTape() as t:
y_sq = y * y
if reset:
# Throw out all of the tape recorded to this point.
t.reset()
z = x * x + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, form=(), dtype=float32)
dz/dy: None
Detener el flujo de gradiente con precisión
En contraste con los controles de cinta globales anteriores, el tf.stop_gradient La función es mucho más precisa. Se puede usar para evitar que los gradientes fluyan a lo largo de una ruta explicit, sin necesidad de acceso a la cinta en sí:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
y_sq = y**2
z = x**2 + tf.stop_gradient(y_sq)
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, form=(), dtype=float32)
dz/dy: None
Gradientes personalizados
En algunos casos, es posible que desee controlar exactamente cómo se calculan los gradientes en lugar de usar el valor predeterminado. Estas situaciones incluyen:
- No hay un gradiente definido para un nuevo OP que está escribiendo.
- Los cálculos predeterminados son numéricamente inestables.
- Desea almacenar en caché un cálculo costoso del pase hacia adelante.
- Desea modificar un valor (por ejemplo, usando
tf.clip_by_valueotf.math.spherical) sin modificar el gradiente.
Para el primer caso, para escribir un nuevo OP que pueda usar tf.RegisterGradient Para configurar el suyo (consulte los documentos API para más detalles). (Tenga en cuenta que el registro de gradiente es international, así que cámbielo con precaución).
Para los últimos tres casos, puede usar tf.custom_gradient.
Aquí hay un ejemplo que se aplica tf.clip_by_norm al gradiente intermedio:
# Set up an id operation, however clip in the course of the gradient cross.
@tf.custom_gradient
def clip_gradients(y):
def backward(dy):
return tf.clip_by_norm(dy, 0.5)
return y, backward
v = tf.Variable(2.0)
with tf.GradientTape() as t:
output = clip_gradients(v * v)
print(t.gradient(output, v)) # calls "backward", which clips 4 to 2
tf.Tensor(2.0, form=(), dtype=float32)
Consulte el tf.custom_gradient Decorador API Docios para más detalles.
Gradientes personalizados en SavedModel
Nota: Esta característica está disponible en TensorFlow 2.6.
Los gradientes personalizados se pueden guardar en SavedModel utilizando la opción tf.saved_model.SaveOptions(experimental_custom_gradients=True).
Para ser guardado en el Modelo Saved, la función de gradiente debe ser rastreable (para obtener más información, consulte el mejor rendimiento con la Guía de Funciones TF).
class MyModule(tf.Module):
@tf.operate(input_signature=[tf.TensorSpec(None)])
def call_custom_grad(self, x):
return clip_gradients(x)
mannequin = MyModule()
tf.saved_model.save(
mannequin,
'saved_model',
choices=tf.saved_model.SaveOptions(experimental_custom_gradients=True))
# The loaded gradients would be the similar because the above instance.
v = tf.Variable(2.0)
loaded = tf.saved_model.load('saved_model')
with tf.GradientTape() as t:
output = loaded.call_custom_grad(v * v)
print(t.gradient(output, v))
INFO:tensorflow:Belongings written to: saved_model/belongings
INFO:tensorflow:Belongings written to: saved_model/belongings
tf.Tensor(2.0, form=(), dtype=float32)
Una nota sobre el ejemplo anterior: si intenta reemplazar el código anterior con tf.saved_model.SaveOptions(experimental_custom_gradients=False)el gradiente aún producirá el mismo resultado en la carga. La razón es que el registro de gradiente todavía contiene el gradiente personalizado utilizado en la función call_custom_op. Sin embargo, si reinicia el tiempo de ejecución después de guardar sin gradientes personalizados, ejecute el modelo cargado debajo del tf.GradientTape lanzará el error: LookupError: No gradient outlined for operation 'IdentityN' (op sort: IdentityN).
Múltiples cintas
Múltiples cintas interactúan sin problemas.
Por ejemplo, aquí cada cinta mira un conjunto diferente de tensores:
x0 = tf.fixed(0.0)
x1 = tf.fixed(0.0)
with tf.GradientTape() as tape0, tf.GradientTape() as tape1:
tape0.watch(x0)
tape1.watch(x1)
y0 = tf.math.sin(x0)
y1 = tf.nn.sigmoid(x1)
y = y0 + y1
ys = tf.reduce_sum(y)
tape0.gradient(ys, x0).numpy() # cos(x) => 1.0
1.0
tape1.gradient(ys, x1).numpy() # sigmoid(x1)*(1-sigmoid(x1)) => 0.25
0.25
Gradientes de orden superior
Operaciones dentro del tf.GradientTape El administrador de contexto se registra para la diferenciación automática. Si los gradientes se calculan en ese contexto, entonces el cálculo de gradiente también se registra. Como resultado, exactamente la misma API también funciona para gradientes de orden superior.
Por ejemplo:
x = tf.Variable(1.0) # Create a Tensorflow variable initialized to 1.0
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
y = x * x * x
# Compute the gradient contained in the outer `t2` context supervisor
# which suggests the gradient computation is differentiable as properly.
dy_dx = t1.gradient(y, x)
d2y_dx2 = t2.gradient(dy_dx, x)
print('dy_dx:', dy_dx.numpy()) # 3 * x**2 => 3.0
print('d2y_dx2:', d2y_dx2.numpy()) # 6 * x => 6.0
dy_dx: 3.0
d2y_dx2: 6.0
Mientras que eso te da la segunda derivada de un escalar función, este patrón no se generaliza para producir una matriz de hessia, ya que tf.GradientTape.gradient Solo calcula el gradiente de un escalar. Para construir una matriz de Hesse, vaya al ejemplo de Hessian bajo la sección jacobiana.
“Llamadas anidadas para tf.GradientTape.gradient“Es un buen patrón cuando calcula un escalar a partir de un gradiente, y luego el escalar resultante actúa como una fuente para un segundo cálculo de gradiente, como en el siguiente ejemplo.
Ejemplo: regularización de gradiente de entrada
Muchos modelos son susceptibles a “ejemplos adversos”. Esta colección de técnicas modifica la entrada del modelo para confundir la salida del modelo. La implementación más easy, como el ejemplo adversario utilizando el ataque del método firmado de gradiente rápido, lleva un solo paso a lo largo del gradiente de la salida con respecto a la entrada; el “gradiente de entrada”.
Una técnica para aumentar la robustez a los ejemplos adversos es la regularización del gradiente de entrada (Finlay y Oberman, 2019), que intenta minimizar la magnitud del gradiente de entrada. Si el gradiente de entrada es pequeño, entonces el cambio en la salida también debe ser pequeño.
A continuación se muestra una implementación ingenua de la regularización de gradiente de entrada. La implementación es:
- Calcule el gradiente de la salida con respecto a la entrada utilizando una cinta inside.
- Calcule la magnitud de ese gradiente de entrada.
- Calcule el gradiente de esa magnitud con respecto al modelo.
x = tf.random.regular([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape() as t2:
# The internal tape solely takes the gradient with respect to the enter,
# not the variables.
with tf.GradientTape(watch_accessed_variables=False) as t1:
t1.watch(x)
y = layer(x)
out = tf.reduce_sum(layer(x)**2)
# 1. Calculate the enter gradient.
g1 = t1.gradient(out, x)
# 2. Calculate the magnitude of the enter gradient.
g1_mag = tf.norm(g1)
# 3. Calculate the gradient of the magnitude with respect to the mannequin.
dg1_mag = t2.gradient(g1_mag, layer.trainable_variables)
[var.shape for var in dg1_mag]
[TensorShape([5, 10]), TensorShape([10])]
Jacobianos
Todos los ejemplos anteriores tomaron los gradientes de un objetivo escalar con respecto a algunos tensores de origen.
La matriz jacobiana representa los gradientes de una función valorada en vector. Cada fila contiene el gradiente de uno de los elementos del vector.
El tf.GradientTape.jacobian El método le permite calcular eficientemente una matriz jacobiana.
Tenga en cuenta que:
- Como
gradient: ElsourcesEl argumento puede ser un tensor o un contenedor de tensores. - A diferencia de
gradient: ElgoalEl tensor debe ser un solo tensor.
Fuente escalar
Como primer ejemplo, aquí está el jacobiano de un objetivo vectorial con respecto a una fuente escalar.
x = tf.linspace(-10.0, 10.0, 200+1)
delta = tf.Variable(0.0)
with tf.GradientTape() as tape:
y = tf.nn.sigmoid(x+delta)
dy_dx = tape.jacobian(y, delta)
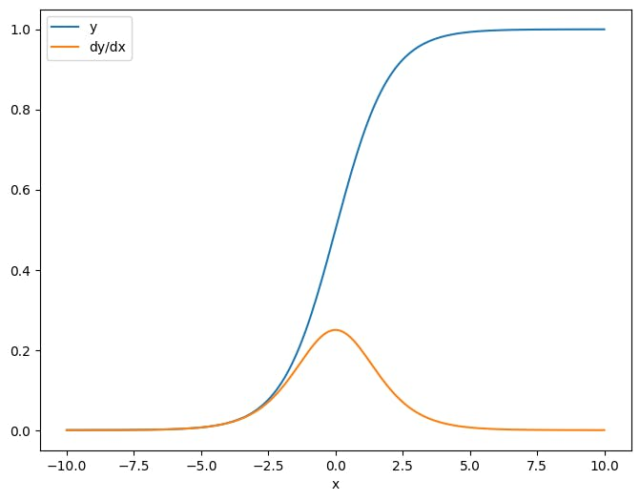
Cuando tomas el jacobiano con respecto a un escalar, el resultado tiene la forma del objetivoy da el gradiente de cada elemento con respecto a la fuente:
print(y.form)
print(dy_dx.form)
(201,)
(201,)
plt.plot(x.numpy(), y, label='y')
plt.plot(x.numpy(), dy_dx, label='dy/dx')
plt.legend()
_ = plt.xlabel('x')
Fuente del tensor
Si la entrada es escalar o tensor, tf.GradientTape.jacobian Calcula eficientemente el gradiente de cada elemento de la fuente con respecto a cada elemento de los objetivos.
Por ejemplo, la salida de esta capa tiene una forma de (10, 7):
x = tf.random.regular([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape(persistent=True) as tape:
y = layer(x)
y.form
TensorShape([7, 10])
Y la forma del núcleo de la capa es (5, 10):
layer.kernel.form
TensorShape([5, 10])
La forma del jacobiano de la salida con respecto al núcleo es esas dos formas concatenadas juntas:
j = tape.jacobian(y, layer.kernel)
j.form
TensorShape([7, 10, 5, 10])
Si suma las dimensiones del objetivo, te queda el gradiente de la suma que se habría calculado por tf.GradientTape.gradient:
g = tape.gradient(y, layer.kernel)
print('g.form:', g.form)
j_sum = tf.reduce_sum(j, axis=[0, 1])
delta = tf.reduce_max(abs(g - j_sum)).numpy()
assert delta < 1e-3
print('delta:', delta)
g.form: (5, 10)
delta: 2.3841858e-07
Ejemplo: Hessian
Mientras tf.GradientTape no da un método explícito para construir una matriz de Hesse, es posible construir uno usando el tf.GradientTape.jacobian método.
Nota: La matriz de Hesse contiene N**2 parámetros. Por esta y otras razones, no es práctico para la mayoría de los modelos. Este ejemplo se incluye más como una demostración de cómo usar el tf.GradientTape.jacobian método, y no es un respaldo de la optimización directa basada en Hessian. Un producto de vector de hessian puede ser
x = tf.random.regular([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.relu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.relu)
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
x = layer1(x)
x = layer2(x)
loss = tf.reduce_mean(x**2)
g = t1.gradient(loss, layer1.kernel)
h = t2.jacobian(g, layer1.kernel)
print(f'layer.kernel.form: {layer1.kernel.form}')
print(f'h.form: {h.form}')
layer.kernel.form: (5, 8)
h.form: (5, 8, 5, 8)
Para usar este Hessian para un paso de método de Newton, primero aplanaría sus ejes en una matriz y aplanaría el gradiente en un vector:
n_params = tf.reduce_prod(layer1.kernel.form)
g_vec = tf.reshape(g, [n_params, 1])
h_mat = tf.reshape(h, [n_params, n_params])
La matriz de Hesse debe ser simétrica:
def imshow_zero_center(picture, **kwargs):
lim = tf.reduce_max(abs(picture))
plt.imshow(picture, vmin=-lim, vmax=lim, cmap='seismic', **kwargs)
plt.colorbar()
imshow_zero_center(h_mat)
El paso de actualización del método de Newton se muestra a continuación:
eps = 1e-3
eye_eps = tf.eye(h_mat.form[0])*eps
# X(ok+1) = X(ok) - (∇²f(X(ok)))^-1 @ ∇f(X(ok))
# h_mat = ∇²f(X(ok))
# g_vec = ∇f(X(ok))
replace = tf.linalg.resolve(h_mat + eye_eps, g_vec)
# Reshape the replace and apply it to the variable.
_ = layer1.kernel.assign_sub(tf.reshape(replace, layer1.kernel.form))
Si bien esto es relativamente easy para un solo tf.Variableaplicar esto a un modelo no trivial requeriría una concatenación y corte cuidadosos para producir una hessia completa en múltiples variables.
Lote jacobiano
En algunos casos, desea tomar el jacobiano de cada uno de un pila de objetivos con respecto a una pila de fuentes, donde los jacobianos para cada par de la fuente de objetivos son independientes.
Por ejemplo, aquí la entrada x está en forma (batch, ins) y la salida y está en forma (batch, outs):
x = tf.random.regular([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = layer2(y)
y.form
TensorShape([7, 6])
El jacobiano completo de y con respecto a x tiene una forma de (batch, ins, batch, outs)incluso si solo quieres (batch, ins, outs):
j = tape.jacobian(y, x)
j.form
TensorShape([7, 6, 7, 5])
Si los gradientes de cada elemento en la pila son independientes, entonces todos (batch, batch) La porción de este tensor es una matriz diagonal:
imshow_zero_center(j[:, 0, :, 0])
_ = plt.title('A (batch, batch) slice')
def plot_as_patches(j):
# Reorder axes so the diagonals will every type a contiguous patch.
j = tf.transpose(j, [1, 0, 3, 2])
# Pad in between every patch.
lim = tf.reduce_max(abs(j))
j = tf.pad(j, [[0, 0], [1, 1], [0, 0], [1, 1]],
constant_values=-lim)
# Reshape to type a single picture.
s = j.form
j = tf.reshape(j, [s[0]*s[1], s[2]*s[3]])
imshow_zero_center(j, extent=[-0.5, s[2]-0.5, s[0]-0.5, -0.5])
plot_as_patches(j)
_ = plt.title('All (batch, batch) slices are diagonal')
Para obtener el resultado deseado, puede sumar el duplicado batch dimensión, o de lo contrario seleccione las diagonales utilizando tf.einsum:
j_sum = tf.reduce_sum(j, axis=2)
print(j_sum.form)
j_select = tf.einsum('bxby->bxy', j)
print(j_select.form)
(7, 6, 5)
(7, 6, 5)
Sería mucho más eficiente hacer el cálculo sin la dimensión adicional en primer lugar. El tf.GradientTape.batch_jacobian El método hace exactamente eso:
jb = tape.batch_jacobian(y, x)
jb.form
WARNING:tensorflow:5 out of the final 5 calls to .f at 0x7f968c10d700> triggered tf.operate retracing. Tracing is dear and the extreme variety of tracings might be because of (1) creating @tf.operate repeatedly in a loop, (2) passing tensors with completely different shapes, (3) passing Python objects as a substitute of tensors. For (1), please outline your @tf.operate outdoors of the loop. For (2), @tf.operate has reduce_retracing=True possibility that may keep away from pointless retracing. For (3), please check with and for extra particulars.
WARNING:tensorflow:5 out of the final 5 calls to .f at 0x7f968c10d700> triggered tf.operate retracing. Tracing is dear and the extreme variety of tracings might be because of (1) creating @tf.operate repeatedly in a loop, (2) passing tensors with completely different shapes, (3) passing Python objects as a substitute of tensors. For (1), please outline your @tf.operate outdoors of the loop. For (2), @tf.operate has reduce_retracing=True possibility that may keep away from pointless retracing. For (3), please check with and for extra particulars.
TensorShape([7, 6, 5])
error = tf.reduce_max(abs(jb - j_sum))
assert error < 1e-3
print(error.numpy())
0.0
Precaución: tf.GradientTape.batch_jacobian Solo verifica que la primera dimensión de la fuente y el destino coincidan. No verifica que los gradientes sean realmente independientes. Depende de usted asegurarse de que solo use batch_jacobian donde tiene sentido. Por ejemplo, agregar un tf.keras.layers.BatchNormalization destruye la independencia, ya que se normaliza a través del batch dimensión:
x = tf.random.regular([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
bn = tf.keras.layers.BatchNormalization()
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = bn(y, coaching=True)
y = layer2(y)
j = tape.jacobian(y, x)
print(f'j.form: {j.form}')
WARNING:tensorflow:6 out of the final 6 calls to .f at 0x7f967c72d430> triggered tf.operate retracing. Tracing is dear and the extreme variety of tracings might be because of (1) creating @tf.operate repeatedly in a loop, (2) passing tensors with completely different shapes, (3) passing Python objects as a substitute of tensors. For (1), please outline your @tf.operate outdoors of the loop. For (2), @tf.operate has reduce_retracing=True possibility that may keep away from pointless retracing. For (3), please check with and for extra particulars.
WARNING:tensorflow:6 out of the final 6 calls to .f at 0x7f967c72d430> triggered tf.operate retracing. Tracing is dear and the extreme variety of tracings might be because of (1) creating @tf.operate repeatedly in a loop, (2) passing tensors with completely different shapes, (3) passing Python objects as a substitute of tensors. For (1), please outline your @tf.operate outdoors of the loop. For (2), @tf.operate has reduce_retracing=True possibility that may keep away from pointless retracing. For (3), please check with and for extra particulars.
j.form: (7, 6, 7, 5)
plot_as_patches(j)
_ = plt.title('These slices usually are not diagonal')
_ = plt.xlabel("Do not use `batch_jacobian`")
En este caso, batch_jacobian todavía se ejecuta y regresa algo con la forma esperada, pero su contenido tiene un significado poco claro:
jb = tape.batch_jacobian(y, x)
print(f'jb.form: {jb.form}')
jb.form: (7, 6, 5)
Publicado originalmente en el